Celowniki torpedowe

Wraz z pojawieniem się nowej broni jaką była torpeda zaistniała konieczność stworzenia systemów kierowania ogniem torpedowym. Podstawowym zadaniem takiego systemu jest wyznaczenie kąta pomiędzy bieżącym namiarem na cel a kierunkiem wystrzelenia torpedy. Wtedy torpeda i poruszający się cel znajdą się w tym samym czasie – w tym samym miejscu – czyli torpeda trafi w cel. W najprostszym przypadku mamy do czynienia z prostoliniowo biegnącymi torpedami wystrzeliwanymi ze stałych oraz obrotowych wyrzutni torpedowych montowanych na pokładach okrętów.

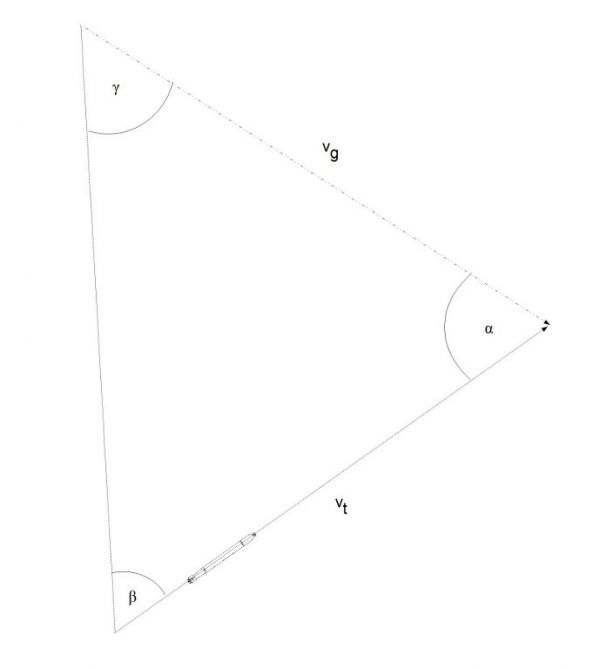
Na powyższym rysunku jest przedstawione wzajemne położenie wyrzutni torpedowej oraz celu, wraz z odległościami oraz kątami.

γ – kąt biegu, niem. Lage (Lagenwinkel), ang. Angle on Bow – kąt pomiędzy kursem celu a linią namiaru na cel, liczony od 0 do 180 stopni w prawo (kąt biegu prawej burty) i w lewo (kąt biegu lewej burty) zaczynając od dziobu okrętu
α – kąt uderzenia torpedy, niem. Schneidungswinkel, ang. Track Angle – kąt pomiędzy kursem celu a linią toru torpedy, liczony od dziobu okrętu
β – kąt strzału torpedy, niem. Vorhalt (Vorhaltwinkel), ang. Deflection Angle – kąt pomiędzy linią namiaru na cel a linią toru torpedy
E – odległość do celu w momencie strzału, niem. Entfernung, ang. Distance
e – długość biegu torpedy, niem. Schußweite, ang. Torpedo Run
v_t – prędkość torpedy, niem. Torpedogeschwindigkeit, ang. Torpedo Speed
v_g – prędkość celu, niem. Gegnerfahrt, ang. Enemy Speed

Załóżmy, że w chwili t₀ wystrzeliwujemy torpedę pod kątem β w stosunku do bieżącego namiaru na cel. Po czasie t torpeda trafia w cel. W tym czasie cel przebył drogę v_g * t, natomiast torpeda przebyła drogę e = v_t * t. Odległości przebyte przez cel oraz przez torpedę są wprost proporcjonalne do prędkości odpowiednio celu oraz torpedy. Powyższy rysunek można zatem przekształcić do następującej postaci:

Stosując do powyższego trójkąta wektorów prędkości twierdzenie sinusów, przy znajomości kąta biegu γ oraz prędkości celu v_g oraz torpedy v_t można wyliczyć kąt strzału torpedy β

czyli

Należy zwrócić uwagę, że do wyznaczenia kąta β nie jest potrzebna odległość do celu E.
Zatem kąt strzału torpedy można było wyliczyć po wykonaniu dwóch działań arytmetycznych oraz dwukrotnym sprawdzeniu tablic wartości funkcji trygonometrycznych – proces prosty, jednak podatny na błędy – zwłaszcza w czasie walki.

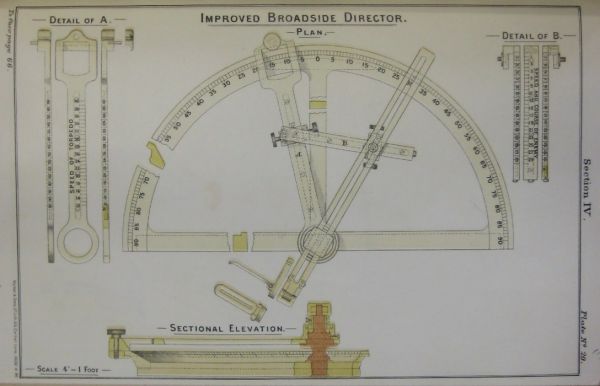
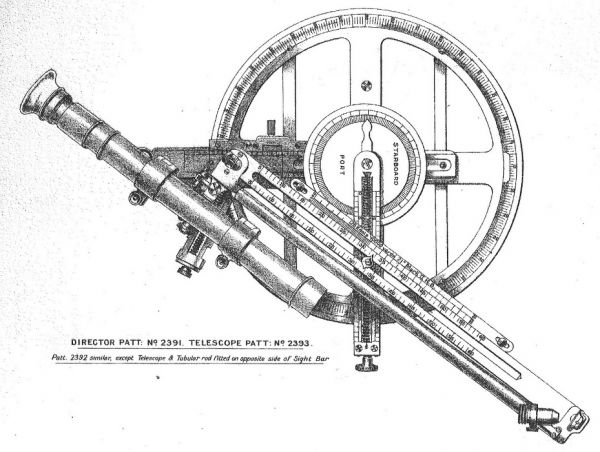
Problem trójkąta torpedowego pomagał rozwiązać prosty celownik mechaniczny instalowany nad wyrzutnią torpedową (niem. Zielapparat, ang. Torpedo Director) . Łączył on w sobie funkcje "kalkulatora" oraz przyrządu do celowania.

Miał on postać trzech linijek – torpedowej T, celowania F oraz celu E - które były wzajemnie ze sobą połączone w ten sposób, że razem tworzyły trójkąt torpedowy. Suwakowe połączenie linijki celowania oraz celu umożliwiało zmianę długości linijki celu w zależności od prędkości celu, natomiast poprzez skracanie lub wydłużanie linijki celowania można było ustawić zakładany kąt biegu. Zakładając, że linijka celowania wskazuje cel, wówczas torpeda powinna zostać odpalona w kierunku wskazywanym przez linijkę torpedową. W praktyce realizowane to było w taki sposób, że linijka torpedowa zawsze wskazywała kierunek strzału wyrzutni, natomiast po ustawieniu prędkości celu i kąta biegu następowało celowanie – albo poprzez obrót wyrzutni torpedowej (w przypadku wyrzutni obrotowych) albo poprzez zmianę kursu okrętu (w przypadku wyrzutni stałych) – tak, aby cel znalazł się na linii wskazywanej przez linijkę celowania.
Początkowo kąt pomiędzy linijką celu oraz linijką celowania był ustawiany na oko, jednak szybko celowniki zaczęto wyposażać w skale umożliwiające dokładne ustawienie kąta biegu.

Z biegiem czasu celowniki torpedowe – zwłaszcza na większych okrętach – krążownikach i pancernikach – zaczęto umieszczać w opancerzonych wieżach dowodzenia lub pomostach bojowych. Miejsca te były umieszczone znacznie wyżej niż wyrzutnie torpedowe, zatem umożliwiały zwykle dogodniejsze warunki obserwacyjne – większy zasięg, nie były przesłaniane przez dymy ze strzelających dział lub rozbryzgi fal. Obsługa celowników była trochę bardziej osłonięta przed ostrzałem nieprzyjaciela, co przekładało się na komfort i dokładność obsługi. Ponadto dzięki temu osiągnięto pewną "centralizację" kierowania ogniem torpedowym – rozwiązanie trójkąta strzału wyznaczane było w jednym miejscu, a nie na każdej wyrzutni – dzięki czemu dane dotyczące kursu celu (prędkość oraz kąt biegu) mogły być przekazywane tylko do jednego miejsca, zamiast do każdej z wyrzutni.
W przypadku okrętu z nieruchomymi wyrzutniami nakazywano wykonanie zwrotu, tak aby cel znalazł się w linii celowania i gdy tak się stało – przekazywano do wyrzutni rozkaz "Pal".
W przypadku wyrzutni obrotowych przekazywano kąt, o jaki należy obrócić wyrzutnie względem podłużnej linii okrętu, a następnie – w momencie gdy cel znalazł się w linii celowania – przekazywano do wyrzutni rozkaz "Pal".

Jednak w przypadku, gdy celownik torpedowy znajduje się w innym miejscu niż wyrzutnia, pojawia się problem paralaksy (niem. Parallaxenfehler) – różnicy kątowej, pod jakim widziany jest cel z miejsca instalacji celownika oraz z wyrzutni torpedowej.

Wielkość tej różnicy kątowej zależy od odległości od celu (im większa odległość, tym różnica kątowa mniejsza) oraz od kąta namiaru na cel (im namiar większy, tymi różnica kątowa większa).
Poprawkę δ wynikającą z paralaksy odczytywano z tablic i dodawano do kąta strzału wyznaczonego przez celownik torpedowy.

W Royal Navy wprowadzono celowniki torpedowe umożliwiające uwzględnienie poprawki na paralaksę przy użyciu dodatkowej linijki, tzw. tangent bar.

Ta dodatkowa linijka znajdowała się w miejscu połączenia linijki torpedowej oraz celowania, umożliwiając przesunięcie punktu obrotu linijki celowania o określoną wartość.
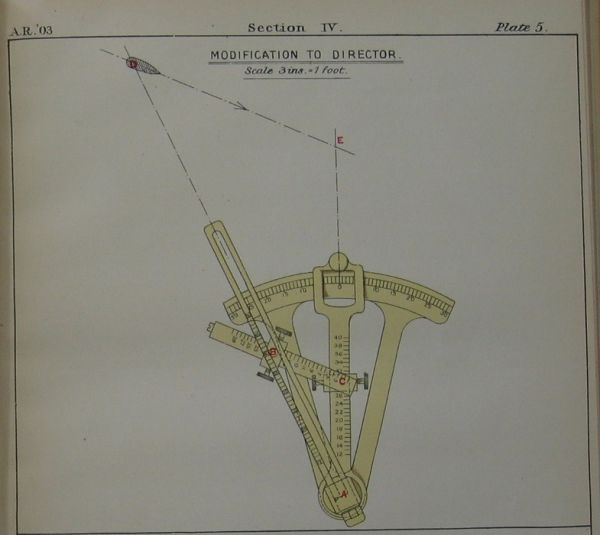
Zasada działania była następująca: załóżmy, że celownik torpedowy jest zainstalowany na pomoście bojowym w punkcie D, w pewnej odległości od wyrzutni torpedowej T. Przeciwnik znajdujący się punkcie E płynie z prędkością v kursem zaznaczonym na rysunku. Gdyby celownik znajdował się na wyrzutni, wówczas linią celowania byłaby linia TE. Gdyby celownik na pomoście ustawiony był tak samo jak na wyrzutni torpedowej, wówczas linia celowania z pomostu wyznaczona byłaby linią DbE' i torpeda wystrzelona w momencie przechodzenia przeciwnika przez celownik opuściłaby wyrzutnię zbyt późno i chybiłaby przechodząc za rufą. Dlatego linia celowania DbE' musi zostać przesunięta tak, aby przechodziła przez punkt E.
Jeżeli teraz narysujemy linię łączącą punkty E i b a następnie przedłużymy ją do przecięcia w punkcie a z linią przechodzącą przez punkty T i D, wtedy linia abE jest linią celowania z uwzględnioną poprawką na paralaksę, a długość odcinka D a wskazuje, o ile należy przesunąć tylny koniec linijki celowniczej.
Z podobieństwa trójkątów: aTE i aDb wynika następująca zależność:

czyli

Db – długość linijki celowniczej
aT – odległość pomiędzy celownikiem na pomoście bojowym a wyrzutnią torpedową
TE – odległość przeciwnika w chwili strzału
Ponieważ wartości Db oraz aT są stałe, długość aD może zostać wyliczona dla każdej wymaganej odległości od przeciwnika, czyli dodatkowa linijka może zostać po prostu wyskalowana w jednostkach odległości od przeciwnika.

W trakcie użytkowania tego typu celowników szybko okazało się, że błędy celowania wynikające z niedokładności szacowania prędkości i kąta biegu przeciwnika są dużo większe niż błąd wynikający z paralaksy, dlatego zarzucono tą komplikację celownika. Dodatkowo często zdarzała się błędna obsługa celownika (np. ustawienie dodatkowej linijki w przeciwną stronę).

Inną poprawką uwzględnianą przy celowaniu z wyrzutni nawodnych było opóźnienie (niem. Befehlsverzug). Był to czas który upływał pomiędzy wydaniem rozkazu odpalenia torpedy a wejściem torpedy do wody a składało się na niego opóźnienie w przekazaniu rozkazu, czas zadziałania mechanizmu spustowego wyrzutni torpedowej, czas opuszczenia wyrzutni przez torpedę a także czas lotu torpedy w powietrzu. Czas ten był istotny przy strzelaniu torped na którąś burtę okrętu. Był on wyznaczany doświadczalnie i wpisywany do odpowiednich tablic. Czas ten w połączeniu z ruchem postępowym okrętu wpływał na przesunięcie rzeczywistego toru ruchu torpedy względem toru wyznaczonego przez celownik torpedowy. Przykładowo, przy opóźnieniu wynoszącym 1 sekundę oraz prędkości okrętu równej 20 węzłów, torpeda wpadała do wody w odległości 10 metrów od linii wyznaczonej przez celownik torpedowy.

Kolejną poprawką była poprawka na prędkość kątową zwrotu wykonywanego przez okręt w trakcie wystrzeliwania torpedy (niem. Winkelgeschwindigkeit). Związana ona była z opóźnieniem rozruchu żyroskopu torpedy. W czasie gdy dysk żyroskopu był rozpędzany, był on blokowany, aby jego oś główna nie przemieszczała się względem głównej osi torpedy. Czas ten wynosił od 0,5 do 0,7 sekundy. Jeżeli okręt wykonywał zwrot z prędkością kątową ω, to przez czas t oś torpedy (razem ze startującym żyroskopem) obróciła się o kąt ω * t względem toru torpedy wyznaczonego przez celownik torpedowy. Przesunięcie punktu przecięcia toru torpedy z torem celu było tym większe, im większa odległość do celu. Przykładowo, przy czasie opóźnienia wynoszącym 0,5 sekundy oraz prędkości kątowej zwrotu równej 1º/s, punkt przecięcia przy odległości 1000 metrów przesuwał się o 17 metrów, natomiast przy odległości 3000 metrów – już o 52 metry.
Poprawka ta wyznaczana była na podstawie tablic oraz dodawana do kąta strzału wyznaczonego przez celownik torpedowy.

W trakcie ataku torpedowego istotną kwestią było stwierdzenie, czy cel znajduje się w zasięgu torpedy. Odpowiedź na to pytanie była możliwa po dokonaniu prostej modyfikacji celownika torpedowego polegającej na dodaniu dodatkowej podziałki (niem. Reichwietenlineal, ang. Possible Shot Scale), która była równoległa do linijki celowania.
Początkowo, podziałka była naniesiona bezpośrednio na linijkę celowania, w takich samych jednostkach jak podziałki prędkości torpedy oraz celu.

Z rysunku wynika następująca proporcja:
\[\begin{aligned} \frac{AD}{AE} = \frac{AB}{AC} \end{aligned} \]

AD – odległość do celu w momencie strzału
AE – zasięg torpedy
AB – wartość odczytana z podziałki na linijce celowania
AC – prędkość torpedy

Dla przykładowych danych (prędkość torpedy: 30, wartość odczytana z podziałki na linijce celowania: 40, maksymalny zasięg torpedy: 2000 metrów) otrzymamy:
AD = AB / AC * AE = 40 / 30 * 2000 = 2666 metrów

Oznacza to, że torpeda o zasięgu 2000 metrów dosięgnie celu, jeżeli ten w momencie strzału będzie znajdował się w odległości nie większej niż 2666 metrów.

Jeżeli zasięg i prędkość torpedy przyjmiemy za stałe, wówczas człon AC * AE również będzie stały – czyli odległość do celu w momencie strzału będzie proporcjonalna do wartości na podziałce linijki celowania. Zatem można tę podziałkę od razu nanieść w odpowiednich jednostkach używając do przeskalowania współczynnika AC * AE. Dzięki temu maksymalną odległość do celu w chwili strzału można bezpośrednio odczytać z podziałki, unikając konieczności wykonania obliczeń.

W praktyce podziałka odległości do celu była nanoszona na oddzielną linijkę, która była montowana na linijce celowniczej. Dzięki temu można było z jednym celownikiem użyć różnych rodzajów torped (różniących się zasięgiem oraz prędkością) – poprzez prostą wymianę linijki odległości.

Celowniki torpedowe często ulegały drobnym modyfikacjom, które zwiększały ich funkcjonalność. Wyposażano je np. w lunety celownicze, dodatkowe podziałki kątowe, umożliwiające bezpośrednie odczytanie kąta uderzenia torpedy w cel, luminescencyjne siatki celownicze.

Demonstracja obsługi celownika torpedowego znajduje się tutaj.

Źródła:

[1] Britain Torpedoes Pre-World War II
[2] Antoni Komorowski, Broń torpedowa
[3] Torpedo Director Pattern 1192
[4] Handbook of Torpedo Control, 1916, ADM 186/381
[5] Royal Navy Torpedo Director - 1909
[6] Torpedo Director Pattern 1193
[7] Torpedo Director Pattern 2391
[8] Possible Shot Scale
[9] Torpedo Director
[10] The 1st Class Torpedo Boat The Countess of Hopetoun
[11] United States of America Torpedoes Pre-World War II