Podstawowe elementy składowe kalkulatorów kierowania ogniem
Powstające w okresie międzywojennym mechaniczne kalkulatory torpedowe były coraz bardziej złożonymi urządzeniami obliczeniowymi. Wywodziły się one z układów kierowania ogniem artyleryjskim (takich jak Dreyer Fire Control Table, Admiralty Fire Control Table lub też Argo Clock), jako że problem kierowania ogniem torpedowym jest uproszczonym (bo sprowadzonym do dwóch wymiarów) problemem kierowania ogniem artyleryjskim, zaś sama balistyka torped jest również prostsza niż balistyka pocisków artyleryjskich.
Urządzenia te nazywane będą kalkulatorami, ponieważ w przeciwieństwie do komputerów, przeznaczone były do rozwiązywania jednego, konkretnego problemu a realizowany przez nie "program" (algorytm) był determinowany przez ich konstrukcję (tzn. nie mógł zostać zmieniony bez przekonstruowania urządzenia). Mechaniczne kalkulatory torpedowe zbudowane były z wielu elementarnych mechanizmów odpowiedzialnych za wykonywanie podstawowych działań matematycznych. Mechanizmy te połączone ze sobą w odpowiedni sposób realizują równania matematyczne, które modelują problem ruchu pocisku artyleryjskiego lub torpedy. Gdy cały układ znajdzie się w równowadze, oznacza to, że znalezione zostało rozwiązanie równania. Kilka z tych elementów zostało przedstawionych na pochodzącym z 1953 roku filmie instruktażowym zrealizowanym dla amerykańskiej Marynarki Wojennej. Film przedstawia mechanizmy w kontekście kalkulatorów kierowania ogniem artyleryjskim i przeciwlotniczym, jednak oczywiście są one również stosowane w kalkulatorach torpedowych.
Kilka zdań komentarza do filmu: we fragmencie omawiającym krzywki pada istotne stwierdzenie - krzywka generuje wartość funkcji dla każdej wartości wejściowej. Innymi słowy, zbiór wartości wejściowych (dziedzina) a także zbiór wartości wyjściowych jest ciągły. W istocie swej bowiem mechaniczne kalkulatory kierowania ogniem były analogowymi maszynami obliczeniowymi - w przeciwieństwie do cyfrowych komputerów operujących na wartościach dyskretnych.
Rozpatrując funkcje przedstawionych na filmie elementów, nasuwają się na myśl porównania z ich odpowiednikami w komputerach cyfrowych.
Odpowiednikami wałów przekazujących wartości są szyny danych, odpowiednikiem przekładni o przełożeniu innym niż 1:1 (czyli dzielenia lub mnożenia przez stałą) - przesunięcie bitów w prawo lub w lewo.
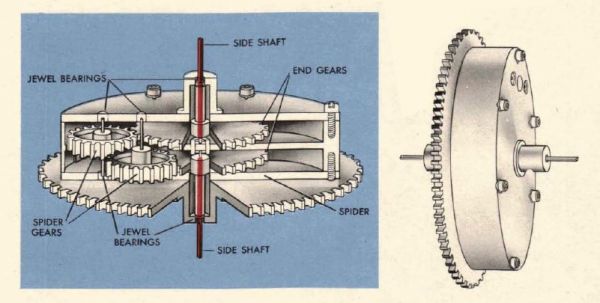
Odpowiednikiem układu różnicowego jest cyfrowy sumator zrealizowany jako układ kombinacyjny.
Krzywki mogą być rozpatrywane jako generatory funkcji lub też jako tablice wartości przechowywane w pamięci ROM, indeksowane wartościami wejściowymi.
Odpowiednikiem układu mnożącego jest cyfrowy układ mnożący zrealizowany jako układ kombinacyjny.
Układy całkujące realizowane są w technice cyfrowej programowo - stosując całkowanie numeryczne. Podobnie jest z układami rozkładającymi wektory na składowe.
Przedstawione na filmie przekładnie różnicowe zbudowane w oparciu o stożkowe koła zębate są stosunkowo mało zwarte. Dlatego często wykorzystuje się obiegowe przekładnie różnicowe.
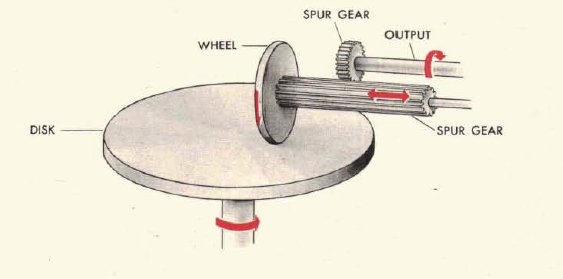
Na filmie przedstawiony został układ całkujący, w którym ruch tarczy był przenoszony wałek przy pomocy przekładni o przełożeniu 1:1 zbudowanej z dwóch kulek umieszczonych w ruchomym wózku. Często stosowane są prostsze układy całkujące, w których układ dwóch kulek został wyeliminowany - wałek wyjściowy jest napędzany bezpośrednio od dysku. W zasada działania obydwu tych układów jest taka sama, natomiast różnica polega na tym, że w układzie całkującym z wałkiem napędzanym bezpośrednio występuje większe tarcie które znacząco ogranicza prędkość działania układu. Dlatego ten rodzaj układu jest stosowany tam, gdzie szybkość zmian zmiennych modelowanego problemu jest niewielka - np. w kalkulatorze kierowania ogniem torpedowym. Natomiast bardziej złożone - ale i szybsze - układy całkujące z przekładnią kulową są stosowane w układach kierowania ogniem artyleryjskim i przeciwlotniczym.
Poniżej omówione zostanie kilka dodatkowych elementów nie przedstawionych w filmie, które jednak również były powszechnie używane w kalkulatorach kierowania ogniem.
Wskaźniki zegarowe służą do wskazywania wartości liczbowych. Mają zastosowanie przy wprowadzaniu danych do kalkulatora, jak również przy prezentacji wyników obliczeń. Generalnie zegarowe tarcze wskaźnikowe miały dwie postacie:
- z nieruchomą tarczą i poruszającą się (obracającą) na jej tle wskazówką. Taki rodzaj tarczy może być zrealizowany na dwa sposoby:
- wskazówka obraca się na osi umieszczonej na środku tarczy
- wskazówka umieszczona jest na obrotowym pierścieniu znajdującym się na krawędzi tarczy - z obrotową tarczą i nieruchomą wskazówką. Ten rodzaj tarczy również może być zrealizowany na dwa sposoby:
- obrotowa tarcza obracająca się na osi umieszczonej na środku tarczy
- obrotowa tarcza ma postać pierścienia
Gdy zachodzi konieczność przedstawienia jakiejś wartości z dużą dokładnością (np. podczas wprowadzania kursu celu), stosuje się podwójne tarcze zegarowe - precyzyjną i zgrubą (ang. fine/coarse, niem. fein/grob). Są one tak ze sobą sprzężone, że ich wskazówki (lub tarcze) poruszają się analogicznie jak minutowa i godzinowa wskazówka zegarowa. Wskazówka (lub tarcza) precyzyjna wykona jeden cały obrót, w czasie gdy wskazówka (lub tarcza) zgrubna - jedynie jego część. Większość wskaźników kursu jest zrealizowana w ten sposób, że wskaźnik zgrubny jest wyskalowany co 5° a jego pełny zakres to 360°. Wskaźnik precyzyjny jest natomiast wyskalowany co 5‘, a jego pełny zakres to 10°. Wał wejściowy służący do wprowadzania wartości jest połączony ze wskaźnikiem precyzyjnym, natomiast wskaźnik zgrubny jest napędzany od wskaźnika precyzyjnego przez przekładnię o przełożeniu 1:36.
Nieco inną odmianą wskaźnika pokazującego kurs jest wskaźnik zespolony, zbudowany z obrotowej tarczy wewnętrznej oraz obrotowego pierścienia zewnętrznego. Obrotowy pierścień jest wyskalowany np. co 10° a jego pełny zakres to 360°, natomiast wewnętrzna tarcza wyskalowana jest co 1°, a jej pełny zakres to 10°.
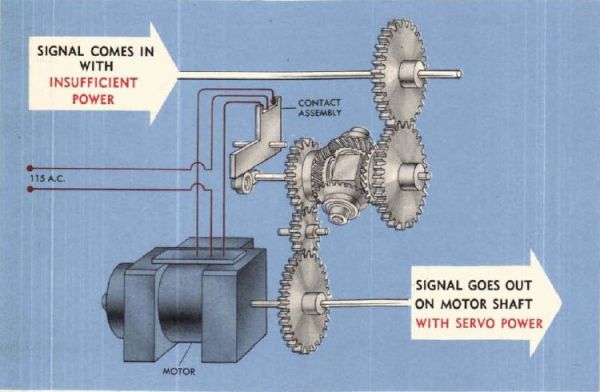
Innymi mechanizmami spotykanymi w kalkulatorach kierowania ogniem są układy nadążne - serwomechanizmy. Wiele elementów składowych kalkulatora (np. układy mnożące, całkujące) nie ma wystarczającej mocy na wałach wyjściowych, aby obracać pozostałe komponenty obliczeniowe. Z powodu mechanicznej natury kalkulatora, na wszystkich przekładniach, łożyskach itp. występują straty, które pochłaniają cześć energii przeznaczonej na poruszanie mechanizmów. Dlatego stosuje się serwomechanizmy, które zwiększają moc wyjściową komponentów kalkulatora tam, gdzie jest to konieczne. Serwomechanizm jest używany w następującej konfiguracji: wał wyjściowy komponentu obliczeniowego (np. układu mnożącego) nie obraca bezpośrednio innych mechanizmów kalkulatora, ale steruje obrotami silnika elektrycznego, który "naśladuje" obrót wału wyjściowego, wprowadzając do układu wzmocnienie kosztem energii elektrycznej zasilającej silnik.
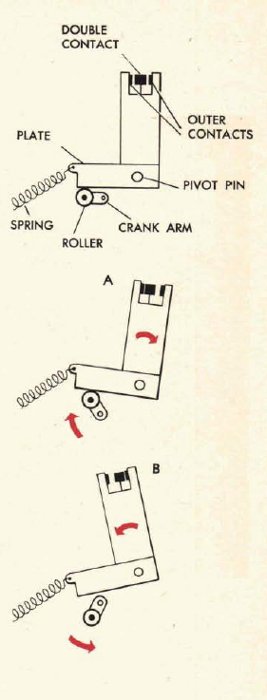
Układ nadążny zbudowany jest z silnika elektrycznego, przekładni różnicowej oraz układu sterującego. Wał silnika elektrycznego jest wałem wyjściowym całego układu: komponent obliczeniowy - serwomechanizm. Na jeden z wałów wejściowych mechanizmu różnicowego podłączony jest wał silnika elektrycznego - wał wyjściowy całego układu. Drugi wał wejściowy mechanizmu różnicowego połączony jest z wałem wyjściowym komponentu obliczeniowego. Na wyjściu mechanizmu różnicowego otrzymujemy sygnał błędu - różnicę pomiędzy pozycją wału wyjściowego komponentu obliczeniowego a pozycją wału silnika elektrycznego. Na wale wyjściowym układu różnicowego znajduje się krzywka, która przełącza styki sterujące silnikiem elektrycznym. W zależności od znaku sygnału błędu (czyli kierunku obrotu wału wyjściowego mechanizmu różnicowego), styki sterujące załączają silnik w odpowiednim kierunku. Obracający się silnik elektryczny dąży do zmniejszenia różnicy pomiędzy wartością wyjściową komponentu obliczeniowego a wartością wskazywaną przez wał silnika. Gdy wał silnika obróci się o taką samą wartość o jaką obrócił się wał wyjściowy komponentu obliczeniowego, sygnał błędu będzie równy zero, a krzywa sterująca znajdzie się w położeniu neutralnym, w którym nastąpi wyłączenie silnika elektrycznego.
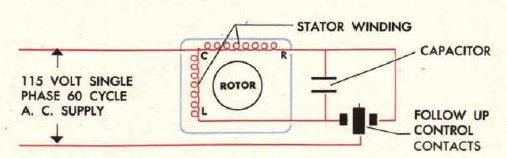
Układ sterowania silnikiem elektrycznym może być zrealizowany na kilka sposobów. Jeden z nich wykorzystuje jednofazowy silnik indukcyjny, posiadający dwa uzwojenia, zamiennie pełniące funkcje uzwojeń rozruchowego i głównego - w zależności od pozycji styków sterujących. Zaletą takiego rozwiązania jest prostota układu - wadą natomiast konieczność zapewnienia źródła napięcia przemiennego.
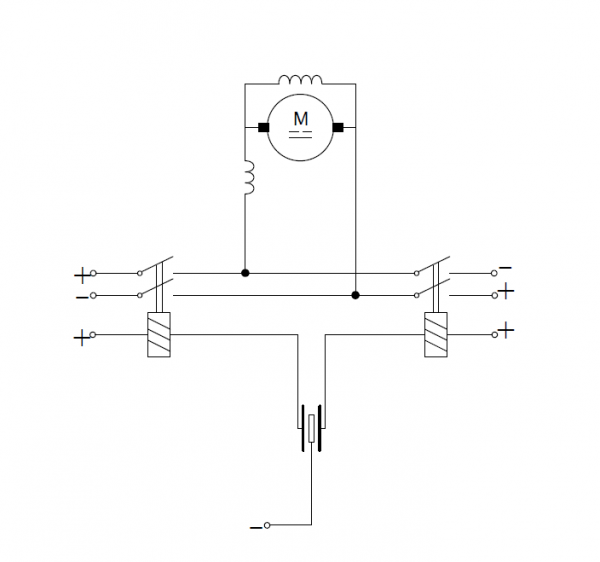
Można także wykorzystać silnik bocznikowy lub bocznikowo-szeregowy prądu stałego sterowany układem przekaźników. Zaletą takiego rozwiązania jest zasilanie układu prądem stałym, natomiast wadą - znaczny stopień złożoności skutkujący większą awaryjnością oraz zajętością miejsca.
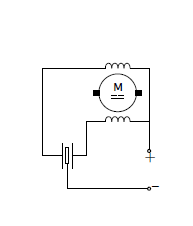
Rozwiązaniem pośrednim może być zastosowanie dedykowanego silnika bocznikowego, który posiada dwa uzwojenia wzbudzania wytwarzające strumienie pola magnetycznego o przeciwnych zwrotach. W zależności od położenia styków sterujących, prąd płynie tylko przez jedno z nich. Złożoność takiego rozwiązania jest porównywalna z rozwiązaniem pierwszym, jednak nie potrzebujemy źródła napięcia przemiennego. Natomiast konieczny jest niestandardowy silnik elektryczny.
Zasada działania układu nadążnego jest wykorzystywana w innym, istotnym elemencie składowym kalkulatora - układzie porównawczym czyli elektromechanicznym komparatorze. Komparatory są konieczne przy realizacji układów rozwiązujących równania. Wytwarzają one sygnał błędu który w pętli sprzężenia zwrotnego wpływa na zmienne równania, dążąc do zrównoważenia obu stron - czyli do znalezienia rozwiązania. Do tego zadania może zostać wykorzystany układ różnicowy, na którego wejścia podawane są wartości obu stron równania. Wyjście układu różnicowego poprzez krzywkę oddziałuje na styki sterujące, które włączają w odpowiednim kierunku silnik elektryczny, zmieniający wartość jednej ze zmiennych równania.
Wydaje się, że taka konstrukcja komparatora została wykorzystana w niemieckim kalkulatorze torpedowym Siemensa.
W amerykańskich układach kierowania ogniem stosowano komparatory działające na zasadzie porównania wzajemnej pozycji ruchomej rolki oraz bębna. Były to tzw. follow-up heads.
Jednym z przykładów użycia komparatora jest implementacja układu dzielącego, zbudowanego z układu całkującego oraz komparatora. Wykorzystana tutaj jest następująca własność układu całkującego: wartość o jaką obróci się wał wyjściowy układu całkującego przy pojedynczym obrocie tarczy jest zależna od pozycji kulki - jej odległości R od środka tarczy i równa jest 2*π*R. Odległość R natomiast jest zależna od jednej z wartości dwóch wartości wejściowych układu całkującego (drugą jest obrót tarczy). Oznaczając symbolami X1, X2 oraz Y odpowiednio wartości wejściowe odpowiedzialne za przesunięcie kulek, obrót tarczy oraz wartość wyjściową widzimy, że:
Y = 2*π*X1*X2
W ten sposób układ całkujący może zostać wykorzystany do realizacji mnożenia dwóch zmiennych, Stałą 2*π można z łatwością wyeliminować przez zastosowanie odpowiedniej przekładni o stałym przełożeniu na wale wyjściowym układu.
Odpowiednie połączenie układu całkującego oraz komparatora umożliwia zrealizowanie dzielenia.
Na wejście układu całkującego podawana jest wartość X1 (dzielnik). Drugie wejście układu jest połączone z silnikiem elektrycznym sterowanym przez komparator. Wartość reprezentowana przez to wejście to X2 - iloraz. Wyjście układu całkującego Y jest równe 2*π*X1*X2. Jest ono połączone z jednym z wejść komparatora. Na drugie wejście komparatora jest podawana wartość którą chcemy podzielić (dzielna).
Chcąc podzielić wartość A przez wartość X1, na wejście komparatora wprowadzamy wartość A, natomiast na jedno z wejść układu całkującego - X1. Na wyjściu układu pojawia się wartość Y = 2*π*X1*X2. Komparator porównuje ją z zadaną wartością A (dzielnej) i wytwarza sygnał sterujący, który odpowiednio włącza silnik elektryczny, który z kolei obraca wałem wprowadzając do układu wartość X2. Silnik elektryczny będzie się obracał aż do chwili, gdy wartość Y zrówna się z wartością A. Wtedy z wału silnika elektrycznego można odczytać wartość X2 która jest szukanym ilorazem.
Komparator może być połączony z zespolonym wskaźnikiem wskazówkowym/tarczowym. Proces porównywania wartości może być wówczas obserwowany wizualnie, a w przypadku awarii układu sterującego lub silnika elektrycznego, dzięki sprzężonym pokrętłom, można ręcznie doprowadzić do zrównania obydwu wartości.
Źródła:
[1] Dreyer Table Mark I
[2] Handbook of The Admiralty Fire Control Clock Mark I and I*
[3] Basic Fire Control Mechanisms - Section 2 - Mechanical Units
[4] Harvey G. Cragon, The Fleet Submarine Torpedo Data Computer
[5] Basic Fire Control Mechanisms - Section 3 - Electromechanical Units
[6] Basic Fire Control Mechanisms - Section 6 - Arma Mechanisms