Pozyskiwanie danych
Kluczową kwestią podczas strzelania torpedami było określenie parametrów kursu celu: kąta biegu, prędkości oraz ewentualnie odległości. Początkowo kurs celu był określany wyłącznie na podstawie obserwacji wzrokowej. Podstawowym ograniczeniem obserwacji wizualnej jest zależność od warunków atmosferycznych oraz pory dnia/nocy. Jednak od połowy Drugiej Wojny Światowej pojawiły się środki techniczne umożliwiające obserwację w nocy oraz w złych warunkach pogodowych – radar oraz sonar.
Stosowano trzy sposoby na określenie parametrów celu na podstawie obserwacji wzrokowej:
- szacowanie “na oko”
- wykonanie nakresu bojowego
- pozyskanie danych z centrali artyleryjskiej (na większych okrętach)
Szacowanie parametrów kursu celu “na oko” było podstawową metodą, ponieważ mogło być użyte w każdej sytuacji i nie wymagało żadnego dodatkowego oprzyrządowania oraz nie było czasochłonne. Dokładność wyników zależała od doświadczenia osoby dokonującej oszacowania.
Prędkość była oceniana na podstawie wielkości odkosów dziobowych i kilwateru. Dodatkową wskazówką – zakładając poprawne rozpoznanie celu - mogła być informacja o zakresie prędkości osiąganych przez cel, odczytana z rejestru statków lub okrętów wojennych. Inną pomocną informacją mogła być prędkość obrotowa śrub – przy znajomości typu statku lub okrętu mogła pomoc w określeniu prędkości celu.
Kąt biegu – czyli kąt pomiędzy kursem celu a linią namiaru na cel - był szacowany na podstawie wyglądu zewnętrznego celu – stopnia skrócenia bocznych powierzchni nadbudówek, wzajemnego usytuowania elementów konstrukcji występujących symetrycznie na obydwu burtach (wentylatorów, żurawików) itp.
Wszelkie potrzebne do szacunków informacje zebrane były w rocznikach flot wojennych oraz rejestrach statków handlowych (np. Weyers Taschenbuch der Kriegsflotten, Die Handelsflotten der Welt, Handbuch der Schiffstypenkunde für die Kriegsmarine, Jane's Fighting Ships). Wydawnictwa te były przygotowywane przez wywiady marynarek wojennych. Przykładowe strony dotyczące niemieckiego pancernika Tirpitz przygotowane przez amerykański wywiad ONI (Office of Naval Intelligence - Biuro Wywiadu Marynarki Wojennej) zawierało między innymi rysunki sylwetek pod różnymi kątami biegu, wymiary jednostki (w tym wysokości masztów) oraz zależność prędkości okrętu od prędkości obrotowej śrub.
Jak wspomniano wcześniej, szacowanie było metodą szybką, ale jej dokładność zależała od doświadczenia osoby oceniającej parametry kursu celu. Była ona stosowana głównie w trakcie ataków z małej odległości, gdy dynamiczne manewry celu uniemożliwiały stosowanie bardziej dokładnych, aczkolwiek czasochłonnych metod, a krótki czas biegu torpedy niwelował ewentualne błędy szacowania kąta biegu oraz prędkości.
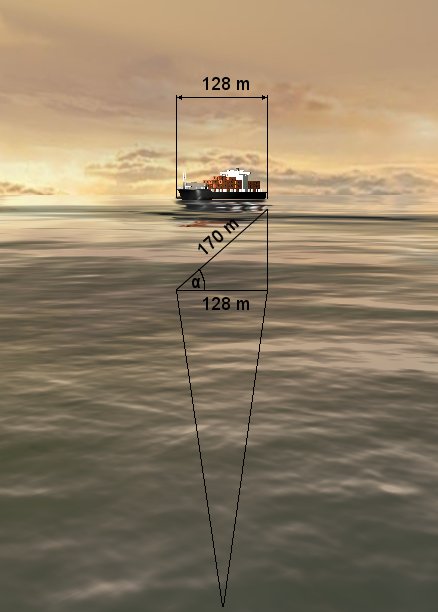
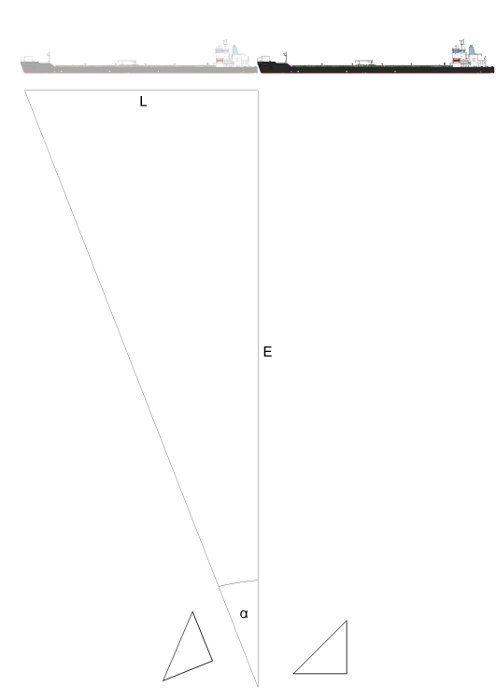
Przy znajomości rzeczywistej długości celu oraz zmierzonej długości obserwowanej (która może być mniejsza ze względu na skrócenie wynikające ustawienia pod kątem innym niż 90°) również można w miarę dokładny sposób wyznaczyć kąt biegu. Jednak metoda ta wymaga już dokonania wykonania pewnych pomiarów. Idea została przedstawiona na poniższych dwóch rysunkach. Pierwszy przedstawia cel widziany pod kątem biegu równym 90° (na bakburtę), a jego zmierzona długość wynosi (załóżmy) Lz = 170 m - i jest równa rzeczywistej długości celu Lr. Drugi rysunek przedstawia cel pod kątem biegu równym 49° (na bakburtę) - jego zmierzona długość wynosi Lz = 128 m. Znając rzeczywistą długość celu (np. z rejestrów statków handlowych), kąt biegu można obliczyć korzystając ze wzoru:
\[\begin{aligned} γ = 90° - α = 90° - arc cos \frac{L_{z}}{L_{r}} = arc sin \frac{L_{z}}{L_{r}} \end{aligned} \]
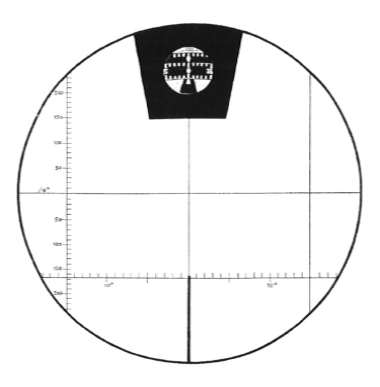
Pomiarów długości (i wysokości) celu w najprostszy sposób dokonywano przy użyciu siatek celowniczych, w które wyposażone były peryskopy oraz celowniki nocne (niem. UZO - U-Boot-Ziel-Optik, ang. TBT - Target Bearing Transmitter). Niemieckie peryskopy Zeissa instalowane na U-Bootach w czasie Drugiej Wojny Światowej posiadały siatkę celowniczą, która miała dwie podziałki: pionową - wyskalowaną w dziesiątkach tysiącznych, oraz poziomą - wyskalowaną w stopniach.
Obliczenie odległości na podstawie wysokości celu odbywało się wg. następującego wzoru:
odległość (w kilometrach) = wysokość celu (w metrach) / wysokość kątowa celu (w tysiącznych)
Dla przykładu, odległość do tonącego frachtowca widocznego na zdjęciu wynosi (zakładając wysokość masztu od linii wodnej - 20 metrów dla statku typu Liberty):
20/120 = około 170 metrów przy powiększeniu 1,5x i około 650 metrów przy powiększeniu 6x.
Znając odległość, można obliczyć długość pozorną celu (która może być mniejsza od rzeczywistej na skutek wpływu kąta biegu):
pozorna długość celu (w metrach) = odległość (w metrach) * tan (długość kątowa celu w stopniach)
Znając długość pozorną celu oraz jego długość rzeczywistą (z rejestrów statków handlowych lub spisów flot), można w opisany wcześniej sposób obliczyć kąt biegu.
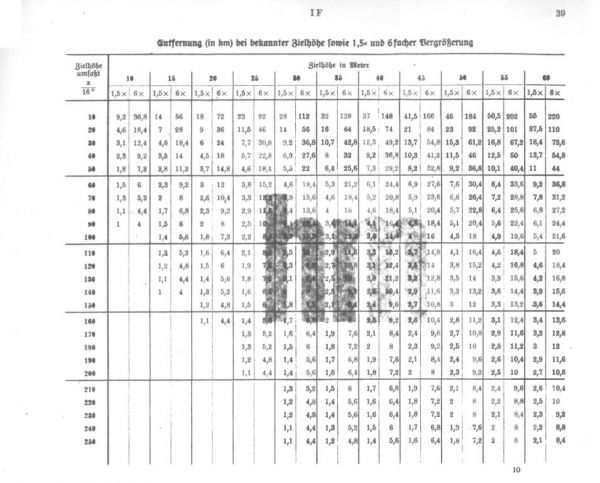
W dodatku do regulaminu M. Dv. 416 Torpedo-Schießvorschrift für U-Boote - w zbiorze tablic M. Dv. 416 Tabellenheft zur Torpedo-Schießvorschrift für U-Boote znajdowały się dwie tablice, które ułatwiały określenie odległości. Pierwsza z nich umożliwiała łatwe określenie odległości do celu (w hm) na postawie jego zmierzonej wysokości (w tysiącznych) oraz zakładanej wysokości w metrach (dla obydwu wartości powiększenia obrazu: 1,5x oraz 6x). Druga tablica umożliwiała określenie odległości do celu (w hm) na podstawie jego zmierzonej długości (w stopniach) oraz zakładanej długości w metrach (dla obydwu wartości powiększenia obrazu: 1,5x oraz 6x). Tablica zawiera wartości dla celu widzianego pod kątem biegu 90°, natomiast na dole strony znajdowały się uwagi, że dla celu widocznego pod kątem biegu 50° oraz 30° odległość wynosi odpowiednio ¾ i ½ wartości odczytanej z tabeli.
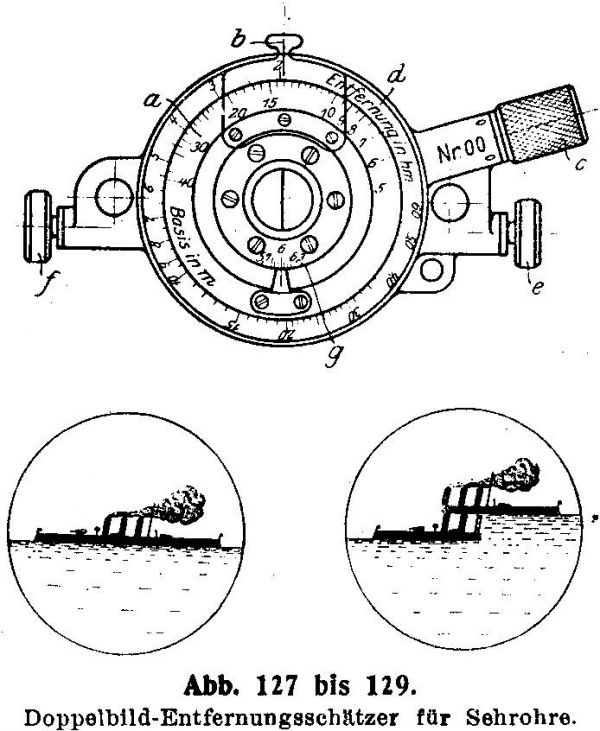
W dwudziestoleciu międzywojennym producenci peryskopów zaczęli wyposażać swoje urządzenia w dalmierze (niem. Doppelbild-Entfernungsmesser, ang. Stadimeter). Z powodu konstrukcji peryskopu (brak bazy optycznej) nie mogły być to dalmierze koincydencyjne ani stereoskopowe. Były to w zasadzie urządzenia, które ułatwiały pomiar wysokości kątowej celu. Po wprowadzeniu zakładanej wysokości celu, na odpowiedniej tarczy można było odczytać odległość. W polu widzenia peryskopu wyposażonego w taki dalmierz widoczne były dwa obrazy celu - jeden nad drugim. Przy pomocy pokrętła należało przesunąć górny obraz tak, aby linia wodna celu na górnym obrazie dotykała wierzchołków masztów celu na dolnym obrazie. Górny obraz był przesuwany w wyniku obrotu dodatkowego pryzmatu. Kąt obrotu tego pryzmatu względem położenia początkowego był równy wysokości kątowej celu i był wskazywany na tarczy dalmierza.
Aby uniknąć konieczności wykonywania dzielenia wysokości celu przez wartość tangensa zmierzonego kąta, tarczę wskazującą wartość kąta wbudowano w prosty przyrząd obliczeniowy, będący rodzajem obrotowego suwaka rachunkowego. Na przedstawionej na fotografii tarczy dalmierza peryskopu 92KA40T/1.99, zewnętrzna tarcza jest ruchoma i obraca się wraz z obrotem pryzmatu (przesunięciem górnego obrazu). Tarcza wewnętrzna jest nieruchoma. Po odpowiednim wzajemnym ustawieniu obydwu obrazów, z wewnętrznej tarczy odczytuje się odległość odpowiadającą wysokości celu.
Dalsza modyfikacja dalmierza peryskopowego umożliwia pomiar kąta biegu celu (niem. Doppelbild-Entfernungs- und Zielkurswinkelschätzer, ang. Range and course-angle finder). Ruchomy pryzmat wytwarzający drugi obraz może zostać obrócony o 90°, dzięki czemu ruchomy obraz znajduje się na poziomie obrazu pierwotnego i może być przesuwany w poziomie. Umożliwia to pomiar długości kątowej celu.
Dalmierz amerykańskiego peryskopu bojowego typu 91KA40T/1.414HA (Type II) zbudowany był z trzech współśrodkowych tarcz. Ruchoma tarcza zewnętrzna posiadała dwie podziałki: przy swej zewnętrznej krawędzi wyskalowaną w stopach, wskazującą długość celu (Length of Target in Feet), oraz przy krawędzi wewnętrznej, wyskalowaną w stopniach, wskazującą kąt biegu (Course Angle).
Tarcza środkowa wyskalowana była w jardach i wskazywała odległość do celu (Range in 100 Yards). Tarcza środkowa obracała się wraz z obrotem pryzmatu wytwarzającego drugi obraz. Nieruchoma tarcza wewnętrzna wyskalowana była w stopach i wskazywała wysokość celu (Height in Feet).
Pomiar odległości i kąta biegu odbywał się następująco: odczytaną z rejestru statków handlowych lub okrętów wojennych długość celu nastawiano obracając zewnętrzną tarczą tak aby była wskazywana przez wskaźnik znajdujący się na dole skali. Początkowo, obydwa obrazy celu - nieruchomy oraz ruchomy - wytwarzany przez obrotowy pryzmat - pokrywały się. Następnie przy pomocy pokrętła regulacyjnego sprzężonego z ruchomym pryzmatem zaczynano rozsuwać obrazy, doprowadzając do tego, aby linia wodna celu na ruchomym obrazie pokryła się ze szczytem masztów obrazu nieruchomego. Przesuwanie obrazu (czyli obrót pryzmatu) powodował obrót środkowej tarczy. Po odpowiednim zgraniu obrazów odczytywano odległość ze środkowej tarczy odpowiadającą wiadomej wysokości celu.
Następnie, w celu pomiaru kąta biegu, kontynuowano rozsuwanie obrazów do momentu kiedy ruchomy obraz zniknął nad górną krawędzią pola widzenia a pokrętło regulacyjne osiągnęło swoje krańcowe położenie. Wówczas mechanizm dokonywał obrotu pryzmatu do takiego położenia, w którym wytwarzany obraz przesuwany był w poziomie. Teraz należało obracać pokrętłem regulacyjnym w kierunku przeciwnym - a ruchomy obraz zaczynał pojawiać się z lewej krawędzi pola widzenia (na tym samym poziomie co obraz nieruchomy) i przesuwał się w kierunku obrazu nieruchomego. Gdy rufa celu na obrazie ruchomym zetknęła się z dziobem celu na obrazie nieruchomym, należało odczytać kąt biegu celu na zewnętrznej tarczy, odpowiadającą zmierzonej w poprzednim etapie odległości na tarczy środkowej.
Kontynuując obrót pokrętła regulacyjnego, doprowadzano do całkowitego pokrycia obrazów ruchomego i nieruchomego. Pokrętło regulacyjne osiągało swoje krańcowe położenie, a mechanizm dokonywał obrotu pryzmatu do położenia początkowego (tzn. do takiego położenia, w którym wytwarzany obraz przesuwany był w pionie) i cykl pomiarowy mógł zostać powtórzony.
Dalmierz niemieckiego peryskopu bojowego typu ASR C/6 zbudowany był z zewnętrznego, nieruchomego pierścienia bazowego (45) (Basis), którego podziałka wyskalowana była w metrach, ruchomego pierścienia środkowego (46) (Entfernung), wyskalowanego w hektometrach oraz ruchomego pierścienia wewnętrznego (52) (Kurswinkel), który był wyskalowany w stopniach. Pierścień środkowy obracał się wraz z obrotem pryzmatu wytwarzającego drugi obraz. Pierścień wewnętrzny był obracany przy pomocy uchwytu (47). Do uchwytu (47) był przymocowany wskaźnik (50), który ułatwiał odczytanie na pierścieniu zewnętrznym wartości odpowiadającej wartości kąta biegu 90° na pierścieniu wewnętrznym. Dodatkowy wskaźnik (48) ułatwiał odczytywanie wartości z pierścienia zewnętrznego i środkowego. Obracany on był niezależnie przy pomocy uchwytu (53).
Pomiar odległości oraz kąta biegu odbywał się następująco: odczytaną z rejestru statków handlowych lub okrętów wojennych wysokość celu nastawiano na zewnętrznym pierścieniu przy pomocy wskaźnika (48), natomiast długość celu - przy pomocy wskaźnika (50). Początkowo, obydwa obrazy celu - nieruchomy oraz ruchomy - wytwarzany przez obrotowy pryzmat - pokrywały się. Następnie przy pomocy pokrętła regulacyjnego sprzężonego z ruchomym pryzmatem zaczynano rozsuwać obrazy, doprowadzając do tego, aby linia wodna celu na ruchomym obrazie pokryła się ze szczytem masztów obrazu nieruchomego. Przesuwanie obrazu (czyli obrót pryzmatu) powodował obrót środkowego pierścienia (46). Po odpowiednim zgraniu obrazów, wskaźnik (48) wskazywał na środkowym pierścieniu (46) odległość do celu (należy podkreślić, że wskaźnik (48) od momentu ustawienia przed rozpoczęciem pomiarów był nieruchomy - to pierścień środkowy się przesuwał pod nim).
Następnie, w celu pomiaru kąta biegu, kontynuowano rozsuwanie obrazów do momentu kiedy ruchomy obraz zniknął nad górną krawędzią pola widzenia a pokrętło regulacyjne osiągnęło swoje krańcowe położenie. Wówczas mechanizm dokonywał obrotu pryzmatu do takiego położenia, w którym wytwarzany obraz przesuwany był w poziomie. Teraz należało obracać pokrętłem regulacyjnym w kierunku przeciwnym - a ruchomy obraz zaczynał pojawiać się z lewej krawędzi pola widzenia (na tym samym poziomie co obraz nieruchomy) i przesuwał się w kierunku obrazu nieruchomego. Gdy rufa celu na obrazie ruchomym zetknęła się z dziobem celu na obrazie nieruchomym, należało odczytać kąt biegu celu na wewnętrznym pierścieniu, który odpowiada zmierzonej w poprzednim etapie odległości na pierścieniu środkowym.
Kontynuując obrót pokrętła regulacyjnego, doprowadzano do całkowitego pokrycia obrazów ruchomego i nieruchomego. Pokrętło regulacyjne osiągało swoje krańcowe położenie, a mechanizm dokonywał obrotu pryzmatu do położenia początkowego (tzn. do takiego położenia, w którym wytwarzany obraz przesuwany był w pionie) i cykl pomiarowy mógł zostać powtórzony.
Demonstracja obsługi takiego dalmierza znajduje się tutaj.
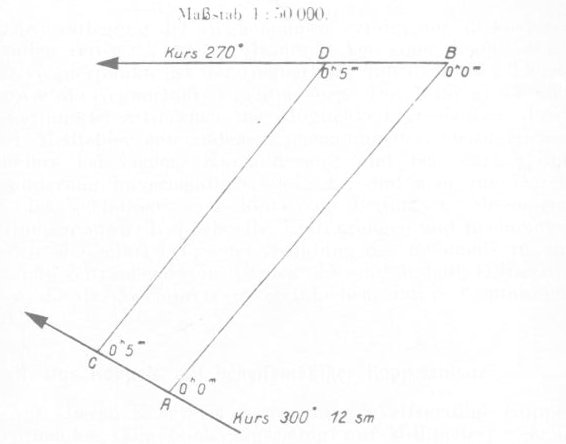
Nakres bojowy (niem. Koppelverfahren, ang. Plotting) był kolejną metodą pozwalającą na określenie parametrów kursu celu. Polegał on na wykonaniu kilku pomiarów odległości wraz z namiarami na cel, oraz naniesieniu ich na planszet (wraz z pozycjami własnego okrętu). Przykładowy nakres jest przedstawiony na rysunku.
W chwili 0h0m własny okręt znajduje się w punkcie A, jego prędkość wynosi 12 węzłów, kurs 300°, namiar na cel wynosi 40°, odległość 10 400 m.
W chwili 0h5m namiar na cel wynosi 38°, odległość 8 900 m.
Pozycje te naniesione zostały na planszet w skali 1:50 000. Najpierw zaznaczono pozycję własnego okrętu w punkcie A. Następnie z tego punktu, pod kątem 40° poprowadzono linię namiaru na cel, gdzie w odległości 20,8 cm zaznaczono pozycję celu (punkt B).
Następnie z punktu A narysowano pod kątem 300° kurs własnego okrętu oraz zaznaczono jego pozycję (punkt C) w 0h5m w odległości 3,7 cm (odległość przebyta w czasie 5 minut z prędkością 12 węzłów, przeliczona do skali 1:50 000). Z punktu C pod kątem 38° poprowadzono linię namiaru na cel i w odległości 17,8 cm zaznaczono jego pozycję (punkt D).
Łącząc punkty B i D otrzymujemy linię kursu celu, który po zmierzeniu wynosi 270°. Odległość pomiędzy tymi punktami została przebyta przez cel w czasie 5 minut. Wynosi ona 5,6 cm w skali planszetu, czyli 2 800 metrów w rzeczywistości. Oznacza to, że cel porusza się z prędkością 18 węzłów. Znając kurs celu oraz namiar na niego oraz kurs własny można było łatwo wyznaczyć jego kąt biegu – mierząc jego wartość na nakresie, korzystając z formuły matematycznej (kąt biegu = kurs celu ± namiar rzeczywisty celu), lub też korzystając z tzw. dysków rachunkowych (niem. Lagenwinkelscheibe).
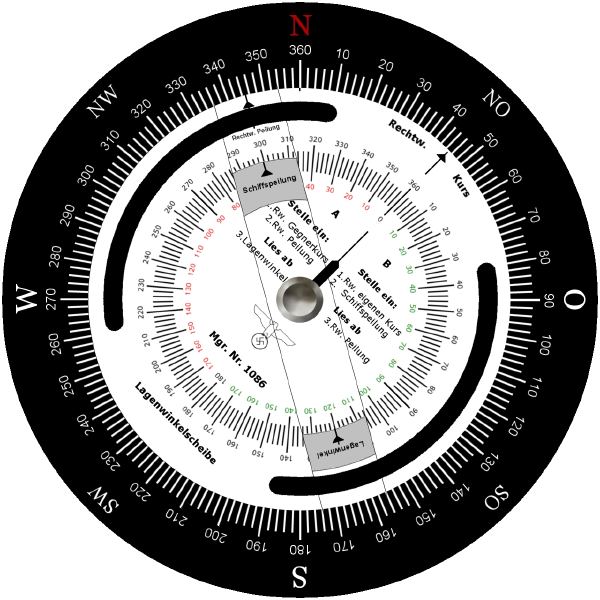
Niemiecki Lagenwinkelscheibe zbudowany był z trzech współśrodkowych tarcz: zewnętrznej tarczy kompasowej (1), tarczy wewnętrznej (2), przeźroczystej tarczy z naniesioną linią odczytu (3). Tarcza kompasowa posiada podziałkę z zakresu 0 do 360°. Tarcza wewnętrzna posiada podziałkę od 0 przez 180° do 0. W zerze posiada skierowaną na zewnątrz strzałkę (4). Linia odczytu (3) posiada trzy znaczniki, które służą do nastawiania lub odczytu namiaru rzeczywistego (5), namiaru względnego (6) i kąta biegu (7).
W celu znalezienia kąta biegu należało wykonać następujące operacje:
1. Nastawić namiar rzeczywisty celu - obracając przeźroczystą tarczą ustawić znacznik (5) na odpowiedniej wartości tarczy kompasowej (1)
2. Nastawić kurs celu – obracając tarczą wewnętrzną (2) ustawić strzałkę (4) na odpowiednią wartość tarczy kompasowej (1)
3. Szukany kąt biegu odczytywany jest z wewnętrznej tarczy (2) pod znacznikiem (7).
Demonstracja obsługi takiego dysku rachunkowego znajduje się tutaj.
W praktyce kolejne pomiary do sporządzenia nakresu bojowego odbywały się częściej (co około 0,5 minuty). Im większa liczba pomiarów (im dłużej prowadzony nakres) – tym dokładniejsze było określenie parametrów ruchu celu. Wadą tej metody była jej pewna czasochłonność (minimalny czas prowadzenia nakresu pozwalający na określenie parametrów kursu wynosił około 5 minut), jednak jej dokładność pozwalała np. na odkrycie schematu zygzakowania celu.
Do określania namiaru na celu używano przeróżnego rodzaju namierników (np. TUZA - Torpedo-U-Boot-Zielapparat, UZO – U-Boot-Ziel-Optik) lub peryskopów. Natomiast pomiaru odległości dokonywano poprzez pomiar rozmiarów kątowych celu (np. wysokości) – czy to przy użyciu siatek pomiarowych czy to przy użyciu dalmierzy pryzmatycznych lub stereoskopowych.
Nakresu bojowego używano nie tylko do wyznaczania kursu pojedynczych jednostek, ale także całych zespołów okrętów lub konwojów. Atak przy użyciu nakresu bojowego zalecany był w warunkach dobrej widoczności, czyli zasadniczo w warunkach dziennych.
W przypadku większych okrętów możliwe było pozyskanie parametrów kursu celu z centrali artyleryjskiej, gdzie zostały obliczone przy pomocy kalkulatorów artyleryjskich, do których dane zostały pozyskane przez dalmierze artyleryjskie i dalocelowniki.
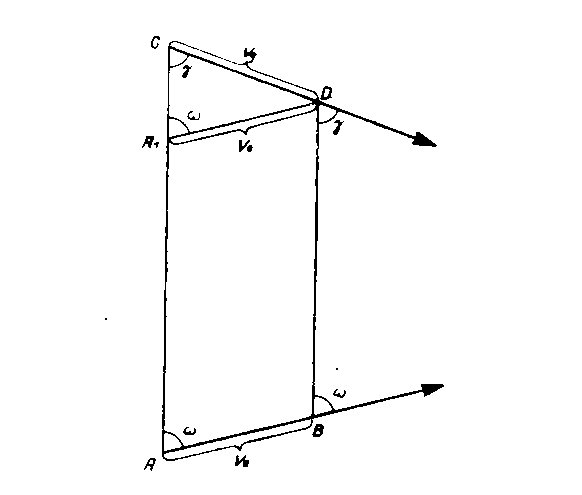
W okresie międzywojennym Niemcy rozwinęli metodę strzelania torped zwaną Ausdampfverfahren. Polegała ona na takim ustawieniu kursu i prędkości własnego okrętu, aby namiar kątowy na cel pozostawał stały (jego zmiany zostały wytłumione, niem. Ausgedampft). Koncepcja tej metody jest przedstawiona na rysunku.
Wektor AB przedstawia kurs własnego okrętu, natomiast prędkość wynosi ve. Kurs celu przedstawia wektor CD, jego prędkość wynosi vg. Prędkość własnego okrętu jest tak dobrana, że namiar na cel ω (w chwilach A i B) pozostaje niezmienny. Kąt biegu γ w punktach C i D jest taki sam.
Celownik torpedowy wyznacza kąt strzału β korzystając z twierdzenia sinusów:
gdzie vg i γ są nieznane.
Na rysunku narysowano odcinek A1D równoległy do odcinka AB i długości równej długości odcinka AB a zarazem wartości prędkości własnego okrętu ve. Kąt przy wierzchołku A1 jest równy ω.
Twierdzenie sinusów zastosowane do tak utworzonego trójkąta A1CD ma postać:
Wartości występujące po prawej stronie równania (prędkość własna oraz namiar na cel) są znane, zatem można je wstawić bezpośrednio do licznika poprzedniego wzoru, otrzymując
W praktyce przeprowadzenie ataku przy użyciu tej metody sprowadzało się do ustawienia kursu i prędkości własnego okrętu tak, aby namiar na cel pozostawał stały. Na celowniku torpedowym prędkość przeciwnika ustawiano na prędkość własnego okrętu, natomiast namiar na cel jako kąt biegu. Następnie wykonywano zwrot całym okrętem (w przypadku nieruchomych wyrzutni) i odpalano torpedy w momencie gdy cel znajdzie się w celowniku, lub też celowano samą wyrzutnią (w przypadku wyrzutni obrotowych).
Metoda ta była zalecana do użycia o zmierzchu oraz w nocy. Nie wymagała pomiarów odległości a jedynie dostosowania własnej prędkości oraz kursu, co zwykle trwało do 10 minut.
Główną wadą metody Ausdampfverfahren był stosunkowo długi czas konieczny do usunięcia zmian namiaru kątowego. Dlatego na jej podstawie rozwinięto inną metodę strzału torpedowego, tzw. Auswanderungsverfahren. Była ona nieco mniej dokładna niż Ausdampfverfahren, ale wymagała jedynie wzięcia dwóch namiarów na cel w odstępie jednej minuty oraz zmierzenia (oszacowania) odległości w trakcie brania pierwszego namiaru.
Istniały dwie wersje tej metody: Auswanderungsverfahren “A” i Auswanderungsverfahren “B”.
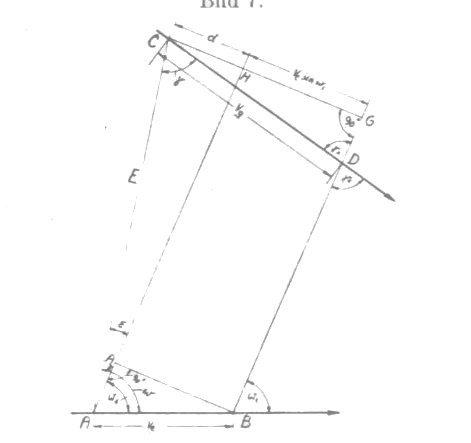
Koncepcja wariantu “A” przedstawiona została na rysunku:
Kurs własny wyznacza prosta AB, prędkość własnego okrętu wynosi ve, kurs przeciwnika wyznacza prosta CD, jego prędkość wynosi vg. W ciągu 1 minuty, własny okręt przemieści się z punktu A do punktu B, natomiast okręt przeciwnika z punktu C do punktu D. Namiar na cel w punkcie A wynosi ω, natomiast w punkcie B wynosi ω1 czyli zmienił się o wartość ε. Innymi słowy, w ciągu 1 minuty namiar na przeciwnika zmienił się o kąt ε.
Celownik torpedowy wyznacza kąt strzału β korzystając z twierdzenia sinusów:
gdzie vg i γ1 są nieznane.
Z rysunku widać, że odcinek CD1 jest równoległy do AB, a odcinek BB1 jest równoległy do AC, więc długość odcinka CB1 = AB = ve, a B1D1 jest równa liniowej zmianie położenia celu d. Długość odcinka CD1 = ve + d, natomiast kąt przy wierzchołku D1 ma wartość ω1.
Ponieważ kąt ω1, prędkość własnego okrętu ve oraz przesunięcie liniowe celu d jest znane, do trójkąta CDD1 można zastosować twierdzenie sinusów:
Wstawiając prawą stronę powyższego wzoru bezpośrednio do licznika poprzedniego wzoru, otrzymujemy:
Na celowniku torpedowym prędkość przeciwnika ustawiano na prędkość własnego okrętu (z poprawką na przesunięcie liniowe celu d), natomiast namiar na cel ω1 jako kąt biegu. To czy przesunięcie liniowe celu d było dodawane lub odejmowane od prędkości własnej ve zależało od tego, czy namiar na cel po upływie 1 minuty się zwiększył czy zmniejszył.
Następnie wykonywano zwrot całym okrętem (w przypadku nieruchomych wyrzutni) i odpalano torpedy w momencie gdy cel znajdzie się w celowniku, lub też celowano samą wyrzutnią (w przypadku wyrzutni obrotowych).
W trakcie pierwszego pomiaru namiaru na cel mierzono (szacowano) również odległość do celu E. Po upływie jednej minuty ponownie mierzono namiar i obliczano zmianę namiaru ε = ω – ω1. Przesunięcie liniowe d obliczano przy użyciu twierdzenia sinusów zastosowanego do trójkąta BB1D1:
Ponieważ wielkość d jest mianowana w jednostkach prędkości (węzłach), natomiast E to odległość mierzona w hektometrach, należało pomnożyć E przez współczynnik 100*60/1820.
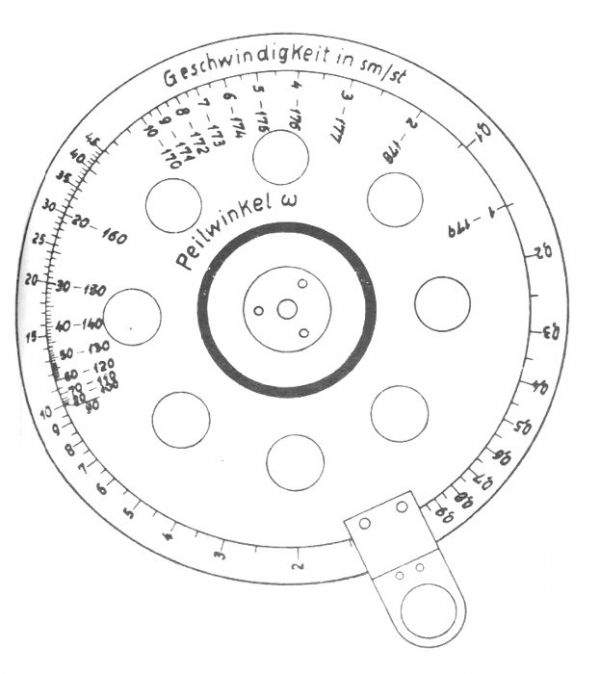
W praktyce obliczanie przesunięcia liniowego d było wykonywane przy pomocy dysku rachunkowego znanego jako Rundschieber für Auswanderungsverfahren “A”. Było to rodzaj suwaka logarytmicznego, posiadającego trzy tarcze i cztery skale. Tarcza zewnętrzna i wewnętrzna są nieruchome, natomiast tarcza środkowa jest obrotowa.
Jego użycie polegało takim wzajemnym ustawieniu tarczy zewnętrznej i środkowej, aby kąt ω1 na środkowej skali odpowiadał kątowi ε na skali zewnętrznej. Przesunięcie liniowe celu d odczytywano na skali wewnętrznej tarczy, przy odpowiedniej wartości odległości E na tarczy środkowej.
Koncepcja wariantu “B” przedstawiona została na rysunku:
O ile w wariancie “A” liniowa zmiana namiaru celu była rzutowana na prostą równoległą do kursu własnego okrętu, tak w wariancie “B” liniowa zmiana namiaru była rzutowana na prostą prostopadłą do linii drugiego namiaru.
Kurs własny wyznacza prosta AB, prędkość własnego okrętu wynosi ve, kurs przeciwnika wyznacza prosta CD, jego prędkość wynosi vg. W ciągu 1 minuty, własny okręt przemieści się z punktu A do punktu B, natomiast okręt przeciwnika z punktu C do punktu D. Namiar na cel w punkcie A wynosi ω, natomiast w punkcie B wynosi ω1 czyli zmienił się o wartość ε.
Celownik torpedowy wyznacza kąt strzału β korzystając z twierdzenia sinusów:
gdzie vg i γ1 są nieznane.
Ponieważ trójkąt CGD jest prostokątny, zachodzi następująca zależność:
Odcinek CG jest rzutem prędkości celu na prostą prostopadłą do linii namiaru.
Długość odcinka CG wynosi GH + HC = GH + d. Zarówno GH jak i d należy obliczyć.
W trójkącie prostokątnym BA1A zachodzi następująca zależność:
Zatem
Odcinek GH jest rzutem prędkości własnego okrętu na prostą prostopadłą do linii namiaru.
Długość odcinka d można obliczyć z zależności:
Zatem twierdzenie sinusów, na podstawie którego celownik torpedowy wyznacza kąt strzału może przyjąć postać:
Jest ona równoważna następującej postaci wzoru:
Na celowniku torpedowym prędkość przeciwnika ustawiano na składową prędkości własnego okrętu (z poprawką na przesunięcie liniowe celu d), natomiast kąt biegu wynosił 90°. To czy przesunięcie liniowe celu d było dodawane lub odejmowane od składowej prędkości własnej vk zależało od tego, czy namiar na cel po upływie 1 minuty się zwiększył czy zmniejszył.
Następnie wykonywano zwrot całym okrętem (w przypadku nieruchomych wyrzutni) i odpalano torpedy w momencie gdy cel znajdzie się w celowniku, lub też celowano samą wyrzutnią (w przypadku wyrzutni obrotowych).
Podobnie jak w przypadku wariantu “A” tej metody, w trakcie pierwszego określenia namiaru celu mierzono (szacowano) również odległość do celu E. Po upływie jednej minuty ponownie określano namiar i obliczano zmianę namiaru ε = ω – ω1.
Obliczeń wartości vk oraz d dokonywano przy pomocy dysku rachunkowego, tzw. Rundschieber für Auswanderungsverfahren “B”. Na obu stronach dysku naniesione były skale przeznaczone do obliczeń prędkości oraz przesunięcia liniowego.
Na przedniej stronie, na nieruchomej krawędzi zewnętrznej dysku znajduje się skala do ustawiania prędkości własnego okrętu ve oraz obrotowa, wewnętrzna tarcza ze skalą do ustawienia kąta namiaru ω1. Do obrotowej, wewnętrznej tarczy przymocowany jest uchwyt, który po swojej drugiej stronie posiada znacznik do odczytu składowej prędkości vk.
Po drugiej stronie dysku, na nieruchomej zewnętrznej krawędzi znajdują się dwie skale – jedna do odczytu składowej prędkości vk , druga zaś do odczytu wartości przesunięcia liniowego celu d. Również na nieruchomiej części dysku – ale bliżej środka – znajduje się podziałka do nastawienia odległości celu E. Wewnątrz dysku znajduje się obrotowa, wewnętrzna tarcza, na której zaznaczona jest skala do ustawienia kąta ε. Do tej tarczy jest przytwierdzona wskazówka do odczytu przesunięcia liniowego celu d na skali zewnętrznej.
Wariant “B” metody Auswanderungsverfahren (w skrócie Aw-Verfahren B) był zalecany do użycia. W porównaniu z wariantem “A” wydaje się, że jest trochę bardziej skomplikowany – wymaga przeprowadzenia dwóch obliczeń, niemniej wydaje się być mniej podatny na błędy – na celowniku torpedowym wartość kąta biegu jest zawsze stała i równa 90°.
Porównanie metod opracowania parametrów kursu celu
| Metoda | Mierzone wielkości | Czasochłonność | Dokładność | Wymagane wyposażenie | Uwagi |
| Szacowanie | brak | brak | niska | brak | Zwykle używane awaryjnie |
| Nakres bojowy | odległość, namiar kątowy | minimum 10 minut | wysoka | brak | brak |
| Ausdampfverfahren | namiar kątowy, prędkość własna | około 10-15 minut | wysoka | brak | brak |
| Auswanderungsverfahren | namiar kątowy, prędkość własna, odległość | około 1 minuty | średnia | dyski obliczeniowe | brak |
Należy podkreślić, że pomimo tego, że gdy opracowywano wyżej opisane metody, do prowadzenia ognia torpedowego używano głównie proste celowniki torpedowe, to metody te były na tyle uniwersalne, że używano ich także później - w czasie Drugiej Wojny Światowej, gdy w użyciu były złożone kalkulatory torpedowe, np. TVRe S2 Siemensa.
Zestawienie ataków i metod zbierania
parametrów ruchu celu w trakcie Drugiej Wojny Światowej [16]
| Okręt | Data | Metoda | Cel |
Torpedy wystrzelone/trafiły |
| U 47 | 11.12.1939 | Ausdampfverfahren | brak | 2/0 |
| U 47 | 12.12.1939 | Ausdampfverfahren | brak | 2/0 |
| U 48 | 11.10.1940 | Szacowanie | Brandanger | 1/1 |
| U 48 | 11.10.1940 | Szacowanie | Port Gisborne | 1/1 |
| U 48 | 11.10.1940 | Szacowanie | brak | 1/0 |
| U 48 | 11.10.1940 | Szacowanie | brak | 1/0 |
| U 48 | 12.10.1940 | Szacowanie | Davanger | 1/1 |
| U 48 | 17.10.1940 | Szacowanie | Scoresby | 1/1 |
| U 48 | 17.10.1940 | Szacowanie | Languedoc | 1/1 |
| U 48 | 17.10.1940 | Szacowanie | brak | 1/0 |
| U 48 | 18.10.1940 | Szacowanie | Sandsend | 1/1 |
| U 48 | 18.10.1940 | Szacowanie | brak | 1/0 |
| U 48 | 20.10.1940 | Szacowanie | Shirak | 1/1 |
| U 100 | 8.12.1940 | Szacowanie | brak | 1/0 |
| U 100 | 8.12.1940 | Szacowanie | brak | 1/0 |
| U 100 | 14.12.1940 | Szacowanie | Kyleglen | 1/1 |
| U 100 | 14.12.1940 | Szacowanie | Euphorbia | 1/1 |
| U 100 | 14.12.1940 | Szacowanie | brak | 1/0 |
| U 100 | 14.12.1940 | Szacowanie | brak | 1/0 |
| U 100 | 14.12.1940 | Szacowanie | brak | 1/0 |
| U 100 | 18.12.1940 | Szacowanie | Napier Star | 2/1 |
| U 100 | 18.12.1940 | Szacowanie | brak | 1/0 |
| U 100 | 22.12.1940 | Szacowanie | brak | 2/0 |
| U 138 | 16.09.1940 | Ausdampfverfahren | brak | 1/0 |
| U 138 | 20.09.1940 | Szacowanie | New Sevilla | 1/1 |
| U 138 | 20.09.1940 | Szacowanie | Boka | 1/1 |
| U 138 | 20.09.1940 | Szacowanie | City of Simla | 1/1 |
| U 138 | 21.09.1940 | Ausdampfverfahren | Empire Adventure | 1/1 |
| U 435 | 17.03.1943 | Szacowanie | William Eustis | 2/1 |
| U 435 | 17.03.1943 | Szacowanie | brak | 2/0 |
| U 435 | 17.03.1943 | Szacowanie | brak | 2/0 |
| U 435 | 17.03.1943 | Szacowanie | brak | 1/0 |
| U 552 | 1.11.1941 | Ausdampfverfahren | brak | 4/0 |
| U 552 | 1.11.1941 | Szacowanie, prędkość na podstawie obrotów śrub |
brak | 2/0 |
| U 557 | 29.05.1941 | Ausdampfverfahren | Empire Storm | 1/1 |
| U 557 | 29.05.1941 | Ausdampfverfahren | brak | 1/0 |
| U 557 | 27.08.1941 | Ausdampfverfahren | Segundo | 1/1 |
| U 557 | 27.08.1941 | Ausdampfverfahren | Saugor | 1/1 |
| U 557 | 27.08.1941 | Szacowanie | brak | 1/0 |
| U 557 | 27.08.1941 | Szacowanie | brak | 1/0 |
| U 557 | 27.08.1941 | Szacowanie | brak | 1/0 |
| U 557 | 27.08.1941 | Szacowanie | Tremoda | 1/1 |
| U 557 | 27.08.1941 | Szacowanie | brak | 1/0 |
| U 557 | 27.08.1941 | Szacowanie | Embassage | 1/1 |
| U 628 | 17.04.1943 | Szacowanie | Fort Rampart | 3/2 |
| U 628 | 5.05.1943 | Nakres bojowy | Harbury | 5/1 |
| U 628 | 5.05.1943 | Szacowanie | brak | 1/0 |
| U 952 | 26.02.1944 | Szacowanie, prędkość na podstawie obrotów śrub |
brak | 1/0 |
| U 952 | 26.02.1944 | Szacowanie | brak | 1/0 |
| U 952 | 28.02.1944 | Szacowanie | brak | 2/0 |
| U 952 | 4.03.1944 | Szacowanie | brak | 1/0 |
| U 952 | 10.03.1944 | Szacowanie | brak | 3/0 |
| U 952 | 10.03.1944 | Szacowanie, prędkość na podstawie obrotów śrub |
Wiliam B. Woods | 1/1 |
| U 967 | 26.04.1944 | Szacowanie, prędkość na podstawie obrotów śrub |
brak | 1/0 |
| U 967 | 5.05.1944 | Szacowanie, prędkość na podstawie obrotów śrub |
USS Fechteler | 1/1 |
| U 967 | 5.05.1944 | Szacowanie | brak | 1/0 |
| U 967 | 8.05.1944 | Szacowanie, prędkość na podstawie obrotów śrub |
brak | 1/0 |
Źródła:
[1] ONI-204 GERMAN NAVAL VESSELS
[2] Die Deutsche Wochenschau No 596, 1942
[3] Die Deutsche Wochenschau
[4] Harry Schlemmer, Vom Turmsehrohr zum Optronikmast. Geschichte der Zeiss U-Boot-Sehrohre
[5] Tabellenheft zur Torpedo-Schießvorschrift für U-Boote, 1940
[6] Submarine torpedo fire conrol manual - Duties of the Fire Control Party
[7] Submarine Periscope Manual, Range and Course-Angle Finder
[8] Hans Techel, Der Bau von Unterseebooten
[9] USS Pampanito virtual tour - conning tower
[10] Richard Lakowski, Deutsche U-Boote GEHEIM 1935-1945
[11] Vesikko - Periscope
[12] Torpedoschießvorschrift, Heft 2, Ermittlung der Schußwerte, 1930
[13] Museum of World War II - German Military Collection
[14] Subsim - Kriegsmarine Wiz-Wheel templates released!
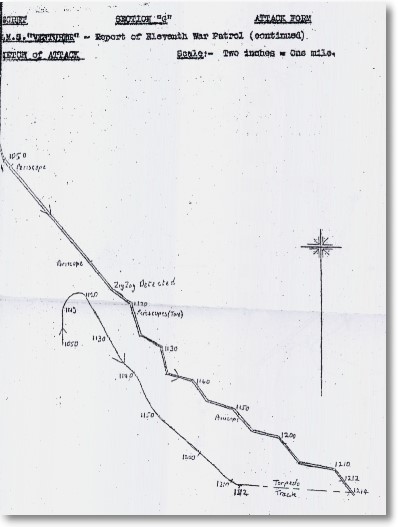
[15] HMS Venturer, Report of Eleventh War Patrol, 1944
[16] Torpedo Schußmeldungen